Index

문제
실행 파일(exe)이 주어지고, 실행하면 사용자 입력을 받고 프로그램이 종료된다.
문제풀이
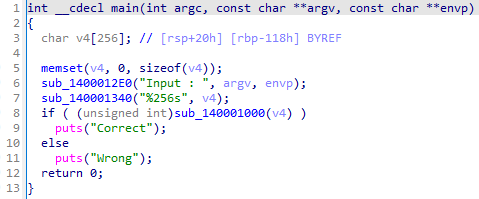
main 함수이다. if 조건문 안의 sub_140001000함수를 확인해보자.
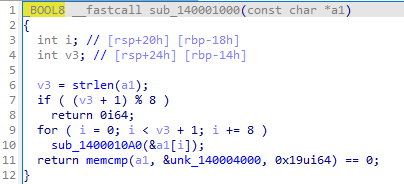
첫 번째 if문을 지나가기 위해서는 사용자 입력 값의 길이가 7의 배수여야 한다.
for문에서는 입력받은 문자열 중, i가 0부터 8씩 증가하면서 입력받은 문자열 끝까지 반복한다.
a1[i]의 주소를 sub_140010a0함수로 넘긴다. sub_140010a0함수가 끝나면 a1의 문자열과 바이너리에 암호화되어 저장된 값인 unk_140004000값과 일치한지 비교한다.
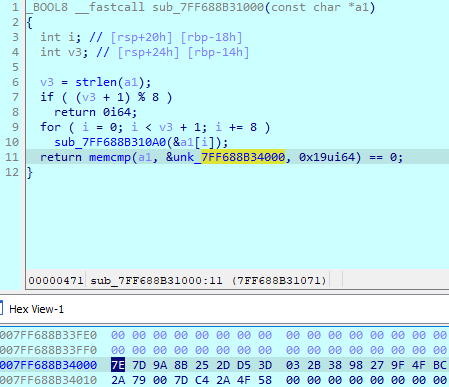
Hex View에서 메모리에 올라간 암호화된 문자열 값을 확인할 수 있다. 우리는 코드를 보고 암호화 로직을 이해하고, 다시 복호화하여 평문 값을 얻으면 된다.
이 값을 비교하기 전인 sub_140010a0함수를 분석해보자. 먼저 8바이트 단위로 배열 특정 인덱스의 주소를 함수로 넘긴다.
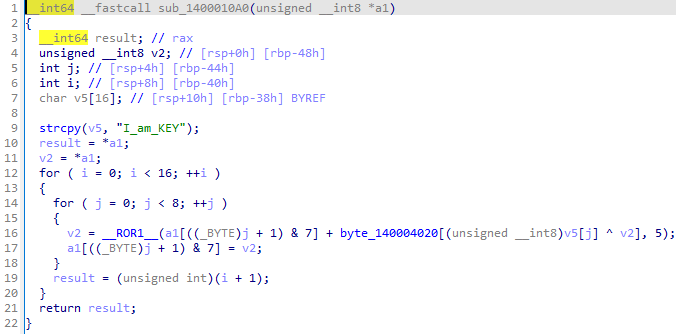
sub_140010a0함수에서는 I_am_KEY라는 문자열을 가지고 사용자 입력을 받은 문자열과 바이너리 안에 저장된 byte_140004020 배열과 ror연산을 수행한다. 앞서 함수에서 for문에서 +=8씩해주는데, 이 함수에서 j로 8바이트만큼 처리를 해주는 것을 확인할 수 있다. 이 사이클을 i값(16번) 만큼 반복한다.
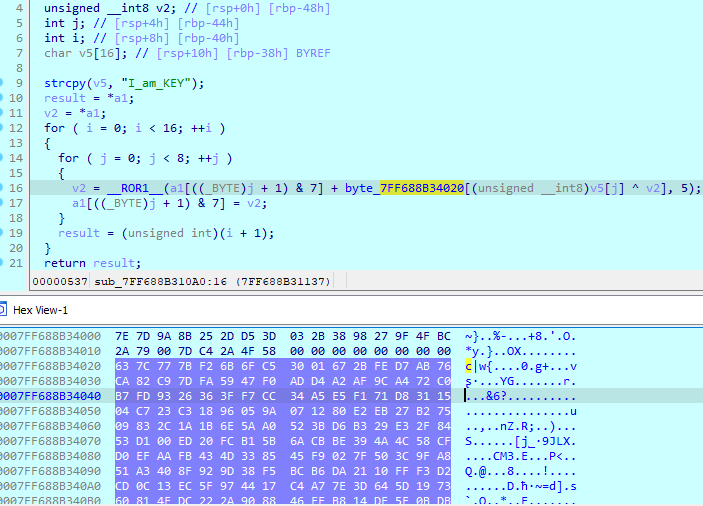
총 256byte로 구성된 배열에 여러 값들이 들어가 있다. I_am_KEY 문자열을 이용해서 이 배열을 참조하면서 암호화를 한다. 우리는 문제에서 암호화된 값을 알고 있으므로, 이 암호화 로직을 반대로 구현하면 된다. 필자는 파이썬 코드를 이용해서 구현했다.
파이썬 풀이 코드
crypt_str = [0x7E, 0x7D, 0x9A, 0x8B, 0x25, 0x2D, 0xD5, 0x3D, 0x03, 0x2B, 0x38, 0x98, 0x27, 0x9F, 0x4F, 0xBC, 0x2A, 0x79, 0x00, 0x7D, 0xC4, 0x2A, 0x4F, 0x58, 0x00]
byte = [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]
str = [0x52, 0x65, 0x76, 0x65, 0x72, 0x73, 0x65, 0x5f, 0x5f, 0x79, 0x6f, 0x75, 0x72, 0x5f, 0x5f, 0x62, 0x72, 0x61, 0x69, 0x6e, 0x5f, 0x3b, 0x29, 0x0]
def ror(x, y): #1byte ror
shr = x >> y
under = x << (8-y)
under &= 0xff
return shr|under
def rol(x, y): #1byte rol
shl = x << y
shl &= 0xff
carry = x >> (8-y)
return shl|carry
def encrypt(a):
key = b'I_am_KEY'
v2 = a[0]
for i in range(16):
for j in range(8):
v2 = ror((a[(j + 1) & 7] + byte[key[j] ^ v2]) & 0xff, 5)
a[(j + 1) & 7] = v2
return a
def decrypt(a):
key = b'I_am_KEY'
for i in range(16):
for j in range(7, -1, -1):
v2 = a[(j + 1) & 7] & 0xff
a[(j + 1) & 7] = (rol(v2,5) - byte[key[j]^a[j & 7]]) & 0xff
return a
result = []
for i in range(0, 24, 8):
#result += encrypt(str[i:i+8])
result += decrypt(crypt_str[i:i+8])
for i in range(len(result)):
print(chr(result[i]), end='')rev-basic-7 문제에서 ror과 rol의 개념과 구현 코드를 알아봤으므로, 여기서는 설명을 건너뛴다. encrypt 함수는 IDA에서 확인한 로직 그대로를 파이썬으로 구현한 것이다. 복호화 코드만 보게되면 반대 로직을 짠 것이 이해하기 힘들 수 있으므로, 작성해두었다. str배열은 플래그의 ascii 코드 값이다. 여기서 중요한 것은 파이썬에서 자료형을 알아서 맞춰주기 때문에, & 0xff연산을 통해 1byte만 남도록 해준 것을 이해할 수 있어야 한다. 그 값에 따라 결과 값이 달라질 수 있기 때문이다. 또한, 암호화때 ror연산을 했으니 복호화땐 rol연산을 수행하고, byte 배열 참조 부분은 암호화시 a[(j+1)&7]에 기존의 v2였던 a[j&7](현재 시점 기준)을 사용하기 때문에 복호화시 a[j&7]을 key[j]와 xor연산을 해준다.
0xff을 and 연산을 해주지 않아 다른 값이 나와서 고생했다..
C로 짜면 조금 더 수월하게 이해하고 풀 수 있을 것 같다.
Uploaded by N2T